L'activitat científica
La investigació científica, magnituds escalars i vectorials, anàlisi dimensional, errors en la mesura i expressió de resultats
Foto de Hans Reniers a Unsplash
Índex
La investigació científica
La investigació científica és el procés pel qual, mitjançant l’aplicació del mètode científic, s’aconsegueix ampliar el coneixement o donar solució a problemes científics.
Saps en què consisteix un doctorat o Ph.D. per les seves sigles en anglès? Descobreix-ho aquí
Imagina un cercle que conté tot el coneixement de la humanitat:
Quan acabes l’escola, saps una miqueta:
Quan acabes l’institut, saps una mica més:
Quan et gradues en la universitat, aconsegueixes una especialitat:
Amb un màster aprofundeixes en aquesta especialitat:
La lectura de literatura científica et porta fins a la frontera del coneixement de la humanitat:
Una vegada en el límit, et centres en un tema específic:
Empenys el límit durant uns anys:
Fins que, un dia, el límit cedeix:
I aquesta senyal que has deixat es diu doctorat (Ph.D.):
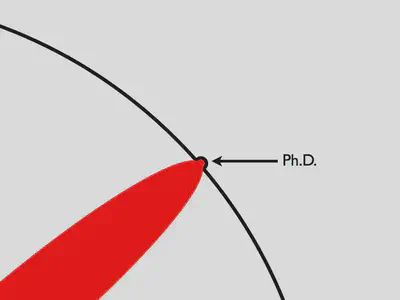
Per descomptat, el món et sembla molt diferent ara:
Però no oblidis prendre perspectiva:
Continua empenyent.
Font: https://ictlogy.net/sociedadred/20100818-guia-ilustrada-para-un-doctorado/
Hipòtesi, lleis i teories
Hipòtesi
Una hipòtesi científica és una proposta d’explicació d’un fenomen, comprovable mitjançant el mètode científic.
Llei
Les lleis científiques són enunciats, basats en experiments o observacions repetides, que descriuen o prediuen una sèrie de fenòmens naturals.
Teoria
Una teoria científica és una explicació d’un aspecte del món natural que pot ser repetidament comprovat i verificat en condicions controlades, d’acord amb el mètode científic.
Magnituds escalars i vectorials
Magnituds escalars
Són aquelles magnituds que queden descrites per un número (escalar) i una unitat.
Exemples
Massa, volum, densitat, temps, temperatura, energia…
Magnituds vectorials
Són aquelles magnituds que queden descrites per:
- Un número (escalar).
- Una unitat.
- Una direcció.
- Un sentit.
- Un punt de aplicació.
Exemples
Posició, desplaçament, velocitat, acceleració, força…
Magnituds bàsiques i derivades
Magnituds bàsiques del SI
El Sistema Internacional d’Unitats (SI) defineix set magnituds bàsiques:
| Magnitud | Unitat | Símbol |
|---|---|---|
| Temps | Segon | s |
| Longitud | Metre | m |
| Massa | Quilogram | kg |
| Corrent elèctrica | Ampere | A |
| Temperatura | Kelvin | K |
| Quantitat de substància | Mol | mol |
| Intensitat lluminosa | Candela | cd |
Magnituds derivades
Les magnituds derivades s’obtenen a partir de dues o més magnituds bàsiques.
Exemples
Superfície, volum, densitat, velocitat, acceleració, força, pressió, energia…
Anàlisi dimensional
L’anàlisi dimensional ens permet relacionar les dimensions (unitats) d’una magnitud derivada amb les de les magnituds bàsiques en les quals es basa.
Equació de dimensions
Les equacions de dimensions són expressions algebraiques en les quals substituïm les magnituds físiques per les seves dimensions (unitats). Per a denotar les dimensions d’una magnitud utilitzem la notació de claudàtors $[\ ]$. Destaquem: \begin{align*} [\text{Massa}] &= \mathsf M \\ [\text{Longitud}] &= \mathsf L \\ [\text{Temps}] &= \mathsf T \end{align*} Sempre que treballem amb equacions de dimensions tractarem d’expressar les dimensions de les magnituds físiques que ens trobem en funció de $\mathsf M$, $\mathsf L$ i $\mathsf T$.
Exemples
$$ [S] = \mathsf{L}^2; [V] = \mathsf{L}^3; [d] = \mathsf{M}\mathsf{L}^{-3}; $$$$ [v] = \mathsf{L}\mathsf{T}^{-1}; [a] = \mathsf{L}\mathsf{T}^{-2}; [F] = \mathsf{M}\mathsf{L}\mathsf{T}^{-2} $$Exemple resolt
Demostra que l’energia cinètica,
$$ E_\mathrm c = \frac{1}{2} m v^2, $$i l’energia potencial gravitatòria,
$$ E_\mathrm p = mgh, $$tenen les mateixes dimensions, on $m$ és massa, $v$ és velocitat, $g$ és l’acceleració de la gravetat i $h$ és altura. Utilitza el resultat per a definir la unitat d’energia en el SI, el juliol (J), en funció de les unitats de massa, longitud i temps del SI.
Analitzem les dimensions de l’energia cinètica $E_\mathrm c$:
$$ \left[E_\mathrm c\right] = \left[\frac{1}{2}mv^2\right] = \left[m\right]\cdot \left[v^2\right] = \mathsf{M}\cdot \left[v\right]^2, $$on hem utilitzat que els números (escalars) no tenen dimensions.
Necessitem conèixer les dimensions de la velocitat:
$$ v = \frac{\Delta x}{\Delta t} \rightarrow \left[v\right] = \frac{\left[\Delta x\right]}{\left[\Delta t\right]} = \frac{\mathsf{L}}{\mathsf{T}} = \mathsf{L}\mathsf{T}^{-1} $$Pel que arribem a:
$$ \left[E_\mathrm c\right] = \mathsf{M}\left(\mathsf{L}\mathsf{T}^{-1}\right)^2 = \mathsf{M}\mathsf{L}^2\mathsf{T}^{-2} $$Analitzem ara les dimensions de l’energia potencial gravitatòria $E_\mathrm p$:
$$ \begin{aligned} \left[E_\mathrm p\right] = \left[mgh\right] &= \left[m\right]\cdot \left[g\right]\cdot \left[h\right] \\\\ &= \mathsf{M}\cdot\left[g\right]\cdot\mathsf{L} \end{aligned} $$Necessitem conèixer les dimensions de l’acceleració $g$:
$$ \begin{aligned} g\equiv a = \frac{\Delta v}{\Delta t} \rightarrow \left[g\right] = \frac{\left[\Delta v\right]}{\left[\Delta t\right]} &= \frac{\mathsf{L}\mathsf{T}^{-1}}{\mathsf{T}} \\\\ &= \mathsf{L}\mathsf{T}^{-2} \end{aligned} $$Pel que arribem a:
$$ \left[E_\mathrm p\right] = \mathsf{M}\cdot\mathsf{L}\mathsf{T}^{-2}\cdot\mathsf{L} = \mathsf{M}\mathsf{L}^2\mathsf{T}^{-2} $$El joule (J) per tant queda definit com:
$$ 1\thinspace\mathrm J = 1\thinspace\mathrm{kg}\thinspace\mathrm{m^2}\thinspace\mathrm{s^{-2}} $$Errors en la mesura
Sempre que es realitza una mesura experimental amb un instrument, aquesta porta associada una incertesa, que fa que sigui impossible obtenir dues mesures exactament iguals. Els errors experimentals són la diferència entre els valors mesurats i els valors reals. Distingim entre errors sistemàtics i errors aleatoris.
Errors sistemàtics i errors aleatoris
Error sistemàtic
Sempre ocorre, amb el mateix valor, quan usem l’instrument de la mateixa manera i en el mateix cas. És predictible i típicament constant o proporcional al valor veritable. Sol ser degut a imperfeccions de l’instrument de mesura o dels mètodes d’observació (inclòs l’observador). Es pot detectar i eliminar.
Error aleatori
Error inevitable que sempre és present en qualsevol mesura. És causat per fluctuacions inherentment impredictibles. Es pot estimar comparant mesures i reduir fent una mitjana de moltes mesures.
Precisió, veracitat i exactitud
Precisió
És la proximitat entre els valors mesurats obtinguts en mesuraments repetits sota condicions similars. És una descripció dels errors aleatoris.
Veracitat
És la proximitat entre la mitjana d’un nombre infinit de valors mesurats repetits i un valor de referència. És una descripció dels errors sistemàtics.
Exactitud
És la proximitat entre un valor mesurat i el valor veritable de la magnitud que es pretén mesurar.
Una alta exactitud és una combinació d’alta precisió i alta veracitat.
.](/media/actividad-cientifica-4ESO/precisio-veracitat-exactitud.svg)
Error absolut i error relatiu
Error absolut
És la diferència entre el valor mesurat i el valor real:
$$ \text{error absolut} = \lvert\text{valor mesurat} - \text{valor real}\rvert $$Té les mateixes dimensions que la magnitud mesurada.
Error relatiu
És el quocient entre l’error absolut i el valor real:
\begin{align*} \text{error relatiu} &= \frac{\text{error absolut}}{\text{valor real}} \\ &= \frac{\lvert\text{valor mesurat} - \text{valor real}\rvert}{\text{valor real}} \end{align*}
És adimensional (sol expressar-se en % multiplicant-ho per 100).
Expressió de resultats
Per regla general, les incerteses sempre s’expressen amb una sola xifra significativa, arrodonint la mesura en conseqüència (unitats, desenes, centenes, etc.).
Exemples
- $t = (5.67\pm 2.00)\thinspace\mathrm s \rightarrow t = (6\pm 2)\thinspace\mathrm s$
- $l = (1307\pm 202)\thinspace\mathrm{\mu m} \rightarrow l = (1300\pm 200)\thinspace\mathrm{\mu m}$
- $m = (437\pm 27)\thinspace\mathrm g \rightarrow m = (440\pm 30)\thinspace\mathrm g$
- $I = (17 \pm 3)\thinspace\mathrm{mA} \rightarrow \text{està ben expressada}$
Rodrigo Alcaraz de la Osa
💼 · 🤝 · 🔗 · ✍️
Soc Doctor en Física per la Universidad de Cantabria i Professor de Física i Química a l’IES Peñacastillo de Cantàbria (Espanya).
Eduard Cremades
📚 Apunts
Soc Doctor en Química i Professor a l’Escola Virolai, a la Universitat Oberta de Catalunya i a la Facultat de Química de la Universitat de Barcelona.
Òscar Colomar
📚 Apunts
Soc Llicenciat en Química i Professor de Secundària a l’IES Isidor Macabich d’Eivissa.
Comparteix-ho
Subscriu-te
Si no vols perdre't cap actualització considera subscriure't al canal de 
Telegram (en espanyol), al canal de 
Whatsapp (en espanyol) o al canal 
RSS.
Discord
Participa activament a la web comentant, donant la teva opinió, realitzant peticions, suggeriments...