Estructura de la matèria

Descarrega aquestes diapositives en format PDF 📥

Models atòmics

(continua cap avall)

👇

Dalton

Basant-se en les idees de Demòcrit, John Dalton va proposar aquest model a principis del segle XIX, considerant l’àtom com una esfera massissa indivisible.

Els descobriments de la radioactivitat natural per Becquerel (1896) i de l’electró per Thomson (1897) van fer necessària la revisió d’aquest model.

Thomson

També conegut com el model del pastís de panses, va ser proposat al 1904 per J.J. Thomson, qui considera que l’àtom està format per un núvol esfèric amb càrrega positiva on es troben incrustats els electrons, amb càrrega negativa, com les panses en un pastís.

Els descobriments del nucli atòmic i del protó per Rutherford (1911 i 1919, respectivament) van portar a la revisió d’aquest model.

Rutherford

Gràcies al seu famós experiment de la làmina d’or (Au), Ernest Rutherford va proposar, al 1911, un model d’àtom format per un nucli, molt petit comparat amb la grandària de l’àtom, amb càrrega positiva i on es concentra gairebé tota la seva massa. Els electrons, amb càrrega negativa, giren al voltant del nucli com ho fan els planetes al voltant del Sol.

La integritat del nucli i la inestabilitat de les òrbites electròniques des d’un punt de vista clàssic van fer necessària la revisió d’aquest model.

Bohr

Proposat al 1913 per Niels Bohr per a explicar l’estabilitat de la matèria i els característics espectres d’emissió i absorció dels gasos.

**Espectre** discret d'**emissió** de l'**hidrogen** (H).
Espectre discret d’emissió de l’hidrogen (H).

Com són els espectres d’emissió de la resta d’elements químics de la taula periòdica?

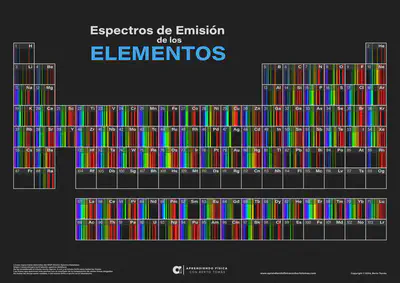
Si vols aprendre més sobre espectres atòmics et recomanem llegir aquesta interessant entrada del blog (en espanyol).

Postulats

Aquest model es basa en tres postulats fonamentals:

  1. Els electrons descriuen òrbites circulars al voltant del nucli sense irradiar energia.
  2. Només estan permeses aquelles òrbites en les quals l’electró té un moment angular múltiple sencer de $\hbar = h/(2\pi)$.
  3. L’electró només emet o absorbeix energia en els salts d’una òrbita permesa a una altra, sent l’energia emesa/absorbida la diferència d’energia entre tots dos nivells.

Ecuación de Rydberg

L’equació de Rydberg ens dóna la longitud d’ona de les línies espectrals de molts elements químics.

Pel cas de l’hidrogen:

$$ \frac{1}{\lambda} = R_\mathrm H\cdot\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right), $$

on $\lambda$ és la longitud d’ona de la radiació emesa en el buit, $R_\mathrm H = 1.097\times 10^7\thinspace \mathrm m^{-1}$ és la constant de Rydberg i $n_1$ i $n_2$ són els nombres quàntics principals de les òrbites involucrades en el salt (amb $n_2>n_1$).

Aquesta equació també ens permet calcular el valor energètic corresponent a una transició electrònica entre dos nivells donats, $\Delta E$:

$$ \Delta E = hcR_\mathrm H\cdot\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right), $$

on $c = 299\thinspace 792\thinspace 458\thinspace \mathrm{m/s}$ és la velocitat de la llum en el buit.

Orígens de la teoria quàntica

(continua cap avall)

👇

Radiació de cos negre

És la radiació electromagnètica re-emesa per un cos ideal que absorbeix tota la radiació que incideix sobre ell (cos negre), estant en equilibri termodinàmic amb el seu entorn.

Un cos negre és qualsevol objecte que absorbeix tota la radiació electromagnètica que incideix sobre ell, re-emetent-la.
Un cos negre és qualsevol objecte que absorbeix tota la radiació electromagnètica que incideix sobre ell, re-emetent-la.

Té un espectre molt característic, inversament relacionat amb la intensitat, que depèn únicament de la temperatura del cos.

La fallida de la teoria clàssica vigent a l’hora d’explicar la forma d’aquest espectre es coneix com la catàstrofe ultraviolada.

Max Planck va ser qui va aconseguir, en 1900, explicar l’espectre del cos negre, donant així origen a la teoria quàntica.

Aprèn més sobre la radiació de cos negre amb aquesta excel·lent simulació:

Hipòtesi de Planck

$$ E = h \nu, $$

on $h = 6.626\times 10^{-34}\thinspace\mathrm{J\thinspace s}$ és la constant de Planck.

Efecte fotoelèctric

L’efecte fotoelèctric consisteix en l’emissió de (foto)electrons quan una radiació electromagnètica, com per exemple llum ultraviolada, incideix sobre un material, típicament metàl·lic.

Característiques

  • La quantitat de fotoelectrons emesos és directament proporcional a la intensitat de la radiació incident.
  • L’emissió de fotoelectrons només es produeix quan la radiació incident té una freqüència major o igual que una certa freqüència mínima, anomenada freqüència llindar o de tall, $\nu_0$, que és característica de cada material.
  • L’energia cinètica dels fotoelectrons depèn únicament de la freqüència de la radiació incident.
  • L’emissió de fotoelectrons es realitza instantàniament, sense existir cap retard entre l’absorció d’energia i l’emissió dels fotoelectrons.

\begin{align*} E &= \phi + E_\mathrm c \\ h\nu &= h\nu_0 + E_\mathrm c \Rightarrow E_\mathrm c = h\left(\nu-\nu_0\right), \end{align*}

on $h = 6.626\times 10^{-34}\thinspace\mathrm{J\thinspace s}$ és la constant de Planck, $\nu$ és la freqüència de la radiació incident, $\nu_0$ és la freqüència llindar (l’energia associada del qual, $\phi = h \nu_0$ es denomina funció de treball o treball d’extracció) i $E_\mathrm c = h\left(\nu-\nu_0\right)$ és l’energia cinètica màxima dels fotoelectrons, emesos sempre que es compleixi $\nu \geq \nu_0$.

Mecànica quàntica

(continua cap avall) 👇

Dualitat ona-corpuscle

Consisteix en el fet que el comportament dels objectes quàntics no pot ser descrit considerant a aquests com a partícules o ones, sinó que tenen una naturalesa dual.

**Electrons** mostrant un **comportament** clarament **ondulatori**, gràcies al famós **experiment** de la **doble escletxa**.
Electrons mostrant un comportament clarament ondulatori, gràcies al famós experiment de la doble escletxa.

A partir d’experiments de difracció d’electrons, Louis de Broglie va ser el primer que va proposar la següent hipòtesi:

$$ \lambda = \frac{h}{mv}, $$

sent $h = 6.626\times 10^{-34}\thinspace\mathrm{J\thinspace s}$ la constant de Planck.

En el següent vídeo de Quantum Made Simple (en anglès) pots aprendre més sobre la dualitat ona-corpuscle:

Principi d’incertesa de Heisenberg

Existeixen uns certs parells de magnituds físiques (aquelles el producte de les quals té dimensions de $\mathsf{M}\mathsf{L}^2\mathsf{T}^{-1}$), que no poden ser determinades simultàniament amb total exactitud, perquè el producte de les seves incerteses ha de ser major o igual que $h/(4\pi) = \hbar/2$.

Exemples de tals magnituds són:

\begin{align*} \text{Posició $x$ i moment linial $p$: } & \Delta x \cdot \Delta p \geq \frac{\hbar}{2} \\ \text{Energia $E$ i temps $t$: } & \Delta E \cdot \Delta t \geq \frac{\hbar}{2} \end{align*}

on $\Delta$ denota la incertesa associada i $\hbar = h/(2\pi)$.

El principi d’incertesa de Heisenberg implica que, encara que s’especifiquin totes les condicions inicials, no és possible predir el valor d’una quantitat amb total certesa, donant així pas a una interpretació probabilística de la mecànica quàntica.

Orbitals atòmics

Són funcions matemàtiques que descriuen la mida, la forma i l’orientació de les regions de l’espai on és possible trobar a l’electró.

Nombres quàntics i la seva interpretació

Els nombres quàntics descriuen valors de magnituds físiques que es conserven en la dinàmica d’un sistema quàntic, com ara l’energia o el moment angular, les quals estan quantitzades i per tant prenen valors discrets.

Per a descriure completament l’estat quàntic d’un electró en un àtom necessitem quatre nombres quàntics, els quals tenen un significat orbital concret.

Nombre quàntic principal $n$

Ens dóna la grandària i la energia de l’orbital. Pren valors naturals ($1\leq n$), com per exemple $n = 1,2,3,\dots$

Nombre quàntic secundari $l$

Ens dóna l’energia i forma de l’orbital. Pot prendre els següents valors:

$$ 0\leq l\leq n-1 $$

de forma que, per exemple, per $n = 3$: $l=\\{0,1,2\\}$.

Nombre quàntic magnètic $m_l$

Ens dóna l’orientació de l’orbital. Pot prendre els següents valors:

$$ -l\leq m_l\leq l $$

de forma que, per exemple, per $l = 2$: $m_l=\\{-2,-1,0,1,2\\}$.

Espín $m_s$

És el moment angular intrínsec. Pot prendre els següents valors:

$$ -s\leq m_s\leq s $$

Per un electró, $s=1/2$, pel que $m_s = \\{-1/2,1/2\\}$.

Coneix més sobre l’espín en aquest magnífic vídeo de Quantum Made Simple (en anglès):

Estructura electrònica

(continua cap avall)

👇

Principi d’exclusió de Pauli

Dos o més electrons no poden tenir tots els seus nombres quàntics idèntics (ocupar el mateix estat quàntic) dins del mateix sistema quàntic (àtom).

Gràcies a aquest principi podem determinar el nombre màxim d’electrons que caben en cada tipus d’orbital:

Tipus d’orbital s p d f
Nombre d’orbitals 1 3 5 7
Nombre màxim d’e– 2 6 10 14

Ordre energètic creixent

La configuració electrònica és la distribució dels electrons d’un àtom en orbitals atòmics (s, p, d i f).

Diagrama de Möller

El diagrama de Möller ens ajuda a saber en quin ordre han d’omplir-se els diferents orbitals, seguint les fletxes (ordre energètic creixent).

Els elements que apareixen aquí en vermell són excepcions. Exemples notables són el Cu ([Ar] 4s1 3d10) i el Cr ([Ar] 4s1 3d5), pel fet que els orbitals d són més estables quan estan plens o semiplens, per raons de simetria.

Regla de Hund de la màxima multiplicitat

En omplir orbitals d’igual energia (per exemple els tres orbitals p) els electrons es distribueixen, sempre que sigui possible, amb els seus espins paral·lels, omplint els orbitals amb la multiplicitat major.

Exemples

Es mostren també els nombres quàntics de l’últim electró:

Partícules subatòmiques

Després dels descobriments de Thomson, Rutherford i Chadwick a principis del segle XX, semblava clar que l’àtom estava format per protons i neutrons en el seu nucli i una escorça on estaven els electrons.

Partícula Massa/kg Càrrega/C
Protó $1.673\times 10^{-27}$ $1.602\times 10^{-19}$
Neutró $1.675\times 10^{-27}$ $0$
Electró $9.109\times 10^{-31}$ $-1.602\times 10^{-19}$
$m_\text{protón}\simeq m_\text{neutrón}\sim 2000m_\text{electrón}$
$q_\text{protón}=-q_\text{electrón}$

Model estàndard

És la teoria que descriu tres de les quatre interaccions fonamentals de la naturalesa conegudes (electromagnètica, nuclear forta i nuclear feble), a més de classificar totes les partícules elementals conegudes.

Evolució de l’Univers

Exportar a PDF

📥 Fes clic aquí i segueix aquestes instruccions:

  1. Obre el diàleg d’Impressió (Control-P si ets al Windows).
  2. Canvia la Destinació a Desa com a PDF.
  3. Canvia el Disseny a Horizontal.
  4. Canvia els Marges a Cap.
  5. Activa l’opció Gràfics de fons.

El procés, en principi, només funciona amb Google Chrome.